บทที่ 3
สำหรับรากที่สองของจำนวนจริงลบจะยังไม่กล่าวถึง เนื่องจากไม่มีจำนวนจริงใดที่ยกกำลังสองแล้วได้จำนวนจริงลบ
ตัวอย่าง
7 เป็นรากที่สองของ 49 เนื่องจาก 72 = 49
-7 เป็นรากที่สองของ 49 เนื่องจาก (-7)2 = 49
บทนิยาม
จากบทนิยาม จะได้ (√(a))2 = a และ (-√(a))2 = a
√a ซึ่งเป็นรากที่สองที่เป็นบวกของ a อาจเรียกอีกอย่างหนึ่งว่า กรณฑ์ที่สองของ a
การหารากที่สองโดยการแยกตัวประกอบ
วิธีทำ
เนื่องจาก 400 = 2 x 2 x 2 x 2 x 5 x 5 = (2 × 2 × 5)2 = 202
400 = (-20)2
ดังนั้น รากที่สองของ 400 คือ 20 และ -20
การหารากที่สองโดยการประมาณ การเปิดตารางและการใช้เครื่องคำนวณ
ตัวอย่างตารางแสดงรากที่สองที่เป็นบวกของจำนวนเต็มบวกมีดังนี้
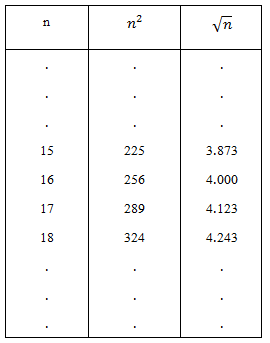
ตามตาราง เมื่อ √n ไม่เป็นจำนวนเต็ม ค่าที่แสดงไว้ในช่อง √n จะเป็นค่าประมาณของจำนวนอตรรกยะ
รากที่สอง
บทนิยาม
ให้ a แทนจำนวนจริงบวกใดๆ หรือศูนย์ รากที่สองของ a คือ จำนวนจริงที่ยกกำลังสองแล้วได้ aสำหรับรากที่สองของจำนวนจริงลบจะยังไม่กล่าวถึง เนื่องจากไม่มีจำนวนจริงใดที่ยกกำลังสองแล้วได้จำนวนจริงลบ
ตัวอย่าง
7 เป็นรากที่สองของ 49 เนื่องจาก 72 = 49
-7 เป็นรากที่สองของ 49 เนื่องจาก (-7)2 = 49
บทนิยาม
ถ้า a เป็นจำนวนจริงบวก รากที่สองของ a มีสองราก คือ รากที่สองที่เป็นบวกซึ่งแทนสัญลักษณ์ √a และรากที่สองที่เป็นลบ ซึ่งแทนด้วยสัญลักษณ์ -√a
ถ้า a = 0 รากที่สองของ a คือ 0จากบทนิยาม จะได้ (√(a))2 = a และ (-√(a))2 = a
√a ซึ่งเป็นรากที่สองที่เป็นบวกของ a อาจเรียกอีกอย่างหนึ่งว่า กรณฑ์ที่สองของ a
การหารากที่สอง
การหารากที่สองของจำนวนจริงทำได้หลายวิธี สำหรับวิธีการคำนวณ นักเรียนจะได้เรียนในระดับชั้นที่สูงกว่านี้ สำหรับในชั้นนี้ นักเรียนอาจใช้การแยกตัวประกอบ การประมาณ การเปิดตาราง และการใช้เครื่องคำนวณ ดังจะได้กล่าวต่อไปนี้
การหารากที่สองโดยการแยกตัวประกอบ
การหารากที่สองโดยการแยกตัวประกอบเป็นสิ่งที่ทำได้ง่าย โดยเฉพาะอย่างยิ่ง การหารากที่สองของจำนวนเต็มบวกที่สามารถแยกตัวประกอบได้ ดังตัวอย่างต่อไปนี้
ตัวอย่าง จงหารากที่สองของ 400วิธีทำ
เนื่องจาก 400 = 2 x 2 x 2 x 2 x 5 x 5 = (2 × 2 × 5)2 = 202
400 = (-20)2
ดังนั้น รากที่สองของ 400 คือ 20 และ -20
การหารากที่สองโดยการประมาณ การเปิดตารางและการใช้เครื่องคำนวณ
นักเรียนเคยทราบมาแล้วว่า ในการหารากที่สองของจำนวนเต็มบวก เมื่อรากที่สองของจำนวนเต็มบวกนั้น ไม่เป็นจำนวนเต็ม ค่าที่ได้จะเป็นจำนวนอตรรกยะ แต่เพื่อความสะดวกในการนำไปใช้ จึงต้องหาค่าประมาณของจำนวนอตรรกยะนั้น
ในกรณีที่จำนวนที่ต้องการหารากที่สองใกล้เคียงกับจำนวนที่สามารถาหารากที่สองได้โดยง่าย ก็จะประมาณรากที่สองของจำนวนนั้นด้วยรากที่สองของจำนวนที่ใกล้เคียง เช่น
15 ใกล้เคียงกับ 16 และ √16 = 4 ดังนั้น √15 ≈ 4
การประมาณข้างต้น เป็นการประมาณรากที่สองที่เป็นจำนวนอตรรกยะด้วยจำนวนเต็ม ถ้าต้องการประมาณเป็นทศนิยม นักเรียนจะได้แนวคิดจากการทำกิจกรรมต่อไปนี้
ตารางรากที่สองตัวอย่างตารางแสดงรากที่สองที่เป็นบวกของจำนวนเต็มบวกมีดังนี้

ตามตาราง เมื่อ √n ไม่เป็นจำนวนเต็ม ค่าที่แสดงไว้ในช่อง √n จะเป็นค่าประมาณของจำนวนอตรรกยะ
ถึงแม้ว่าการหารากที่สอง โดยการเปิดตารางจะทำได้ง่าย ก็ยังมีข้อจำกัดที่ไม่สามารถใช้ในการหารากที่สองของจำนวนจริงบวกได้ทุกจำนวน และไม่สามารถหาเป็นทศนิยมหลายตำแหน่งได้ตามต้องการ วิธีหารากที่สองที่สามารถใช้ได้กับทุกจำนวนจริงบวกและสามารถหาเป็นทศนิยมได้หลายตำแหน่งและสะดวกกว่าการเปิดตาราง คือ การใช้เครื่องคำนวณหรือเครื่องคิดเลข
การหารากที่สองโดยใช้เครื่องคำนวณหรือเครื่องคิดเลข เป็นวิธีที่สะดวกและรวดเร็วมาก แต่เครื่องคำนวณที่ใช้กันอยู่ในปัจจุบันมีหลากหลายชนิด และแต่ละชนิดก็อาจมีวิธีใช้แตกต่างกัน การจะใช้เครื่องคำนวณชนิดใดจึงต้องศึกษาคู่มือการใช้งานของเครื่องนั้น ๆ
แบบทดสอบคณิตศาสตร์ ม.3
1. ค่าของ x จากอสมการ 34(𝑥+2)−23≤𝑥3 ตรงกับข้อใด
1. 𝑥≥2 2. 𝑥≤2 3. 𝑥≥−2 4. 𝑥 ≤−2
2. ค่าของ x จากอสมกา 7(𝑥−5)+10<8(2𝑥+2)−14 ตรงกับข้อใด
1. 𝑥 >−3 2. 𝑥<−3 3. 𝑥>3 4. 𝑥 <3
3. ค่าของ x จากอสมการ 𝑥3−2≥2𝑥3+1 ตรงกับข้อใด
1. 𝑥 ≥−8 2. 𝑥≥8 3. 𝑥≤−9 4. 𝑥 ≤ 9
4. กระปุกออมสินมีเงินอยู่ 17 บาท ซึ่งประกอบด้วยเหรียญห้าสิบสตางค์และเหรียญสลึงนับจำนวนเหรียญรวมกัน
ได้มากกว่า 38 เหรียญ แต่ไม่เกิน 52 เหรียญ จงหาว่าเหรียญแต่ละชนิดมีอย่างน้อยกี่เหรียญและอย่างมากกี่เหรียญ
5. มีสลาก 30 ใบเขียนเบอร์ 1 ถึง 30 สลากทั้งหมดอยู่ในกล่อง สุ่มหยิบขึ้นมา 1 ใบ จงหาความน่าจะเป็นที่จะได้สลากที่หารด้วย
2 หรือ 7 ลงตัว มีค่าเท่ากับข้อใด
1. 512 2. 1730 3. 436 4. 49
6. ในการตรวจหลอดไฟ 3 หลอด ว่าเป็นหลอดดีหรือไม่ จงหาความน่าจะเป็นที่หลอดจะเสียอย่างน้อย 2 หลอด
1. 13 2. 23 3. 38 4. 12
7. ใช้เลข 0 , 1 , 2 สร้างจำนานที่มี 2 หลัก จงหาความน่าจะเป็นที่จะได้เลขคู่ ถ้าใช้เลขไม่ซ้ำกัน มีค่าตรงกับข้อใด
1. 16 2. 13 3. 23 4. 34
8. ทอดลูกเต๋า 2 ลูก 1 ครั้ง ความน่าจะเป็นที่จะได้ผลรวมของแต้มเป็น 5 หรือ 11 มีค่าเท่าไร
1. 112 2. 19 3. 16 4 . 29
9. มีลูกแก้ว 4 ลูกสีต่างๆกัน ต้องการหยิบมาครั้งละ 2 ลูก จะหยิบได้กี่วิธี
1. 6 วิธี 2 . 8 วิธี 3. 10 วิธี 4. 12 วิธี
10. ข้อมูลชุดหนึ่ง คือ 12, 15, 19, 16, 12, 10 ค่าใดต่อไปนี้มีค่ามากสุด
1. มัธยฐาน 2. ฐานนิยม 3. ค่าเฉลี่ยเลขคณิต 4. ค่ากึ่งกลางพิสัย
11. กำหนด x แทนจำนวนเต็มใด ๆ ข้อมูลชุดหนึ่งประกอบด้วย 8, x – 3, 12, 10, x + 1, 13, x + 4 ถ้าค่าเฉลี่ยเลขคณิตเท่ากับ 12 แล้วฐานนิยมเป็นเท่าไร
1. 10 2. 11 3. 12 4. 13
12. ข้อมูลชุดหนึ่ง คือ 15, 13, 8, 10, 9, 19, 5, 9 ข้อใดต่อไปนี้เรียงค่ากลางของข้อมูลชุดนี้จากค่าน้อยไปหาค่ามาก
1. ฐานนิยม มัธยฐาน ค่าเฉลี่ยเลขคณิต 2. ฐานนิยม ค่าเฉลี่ยเลขคณิต มัธยฐาน
3. ค่าเฉลี่ยเลขคณิต ฐานนิยม มัธยฐาน 4. มัธยฐาน ฐานนิยม ค่าเฉลี่ยเลขคณิต
13. ในการตรวจหลอดไฟ 3 หลอด ว่าเป็นหลอดดีหรือไม่ จงหาความน่าจะเป็นที่หลอดจะเสียอย่างน้อย 2 หลอด
1. 13 2. 23 3. 38 4. 12
14. ใช้เลข 0 , 1 , 2 สร้างจำนานที่มี 2 หลัก จงหาความน่าจะเป็นที่จะได้เลขคู่ ถ้าใช้เลขไม่ซ้ำกัน มีค่าตรงกับข้อใด
1. 16 2. 13 3. 23 4. 34
15. ค่าเฉลี่ยเลขคณิตของข้อมูลชุดใดไม่เท่ากับ 12
1. 10, 12, 15, 11 2. 8, 10, 18, 13, 12
3. 13, 15, 10, 9, 11, 14 4. 16, 13, 8, 10, 15, 13, 9
16. กำหนด x แทนจำนวนเต็มใด ๆ ข้อมูลชุดหนึ่งประกอบด้วย 8, x – 3, 12, 10, x + 1, 13, x + 4 ถ้าค่าเฉลี่ยเลขคณิตเท่ากับ 12 แล้วฐานนิยมเป็นเท่าไร
1. 10
2. 11
3. 12 4. 13
17. ข้อมูลชุดหนึ่ง คือ 15, 13, 8, 10, 9, 19, 5, 9
ข้อใดต่อไปนี้เรียงค่ากลางของข้อมูลชุดนี้จากค่าน้อยไปหาค่ามาก
1. ฐานนิยม มัธยฐาน ค่าเฉลี่ยเลขคณิต 2. ฐานนิยม ค่าเฉลี่ยเลขคณิต มัธยฐาน
3. ค่าเฉลี่ยเลขคณิต ฐานนิยม มัธยฐาน 4. มัธยฐาน ฐานนิยม ค่าเฉลี่ยเลขคณิต
18. คะแนนเฉลี่ยของนักเรียน 13 คน เท่ากับ 18 คะแนน ต่อมามีนักเรียนในกลุ่มนี้ลาออกไป 1 คน ทำให้คะแนนเฉลี่ยของ นักเรียนที่เหลือเท่ากับ 17.5 คะแนน จงหาว่านักเรียนที่ลาออกไปมีคะแนนเท่าไร
1. 18 คะแนน 2. 20 คะแนน 3. 21 คะแนน 4. 24 คะแนน
19. ถ้าพื้นที่ผิวของทรงลูกบาศก์รูปหนึ่งเป็น 150 ตารางนิ้ว จงหาว่าลูกบาศก์ดังกล่าวมีความยาวด้านละเท่าไร
ก. 25 นิ้ว ข. 5 นิ้ว
ค. 30 นิ้ว ง. 6 นิ้ว
20. พีระมิดฐานสี่เหลี่ยมจัตุรัสยาวด้านละ 12 เซนติเมตร มีสูงเอียงยาว 10 เซนติเมตร จงหาสูงตรงของพีระมิด
ก. 5 เซนติเมตร ข. 6 เซนติเมตร
ค. 7 เซนติเมตร ง. 8 เซนติเมตร
ไม่มีความคิดเห็น:
แสดงความคิดเห็น